In der Hochfrequenztechnik und somit im Amateurfunk werden an verschiedenen Stellen Induktivitäten eingesetzt. Insbesondere bei Anpassnetzwerken, Filtern und Schwingkreisen. Auch im Antennenbau sind Induktivitäten ein wichtiges passives Bauelement. Das Schaltzeichen sie wie folgt aus:
Die Maßeinheit für die Induktivität ist das Henry (H) und wurde nach dem amerikanischen Physiker Joseph Henry benannt. Das Henry lässt sich auch aus den SI-Basiseinheiten entwickeln und hat dann die Einheit Vs/A. Warum das hier erläutert wird, sehen Sie gleich, wenn eine Luftspule berechnet wird.
Berechnung der Induktivität
Anlass dieser Betrachtung ist der Wunsch, eine Rahmenantenne zum Empfang des Maschinensenders SAQ in Grimeton (Schweden) zu bauen. Die Rahmenantenne ist vom Grundsatz her nichts anderes als eine Luftspule. Die Berechnung sollte daher mit einschlägigen Formeln möglich sein. Eine Formel, die sicherlich auch dem interessierten Laien bekannt sein könnte, beschreibt die Induktivität einer Luftspule wie folgt: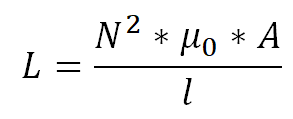 Wobei
Wobei
L = Induktivität in H
N = Windungszahl
µ0 = magnetische Feldkonstante mit ![]()
A = Querschnittsfläche der Spule
l = Länge der Spule
Diese Formel funktioniert allerdings nur, wenn die Länge der Spule deutlich größer als ihr Durchmesser ist. Betrachtet mal Luftspulen , die als Bauelement in einer Schaltung eingesetzt werden sollen, ist dieses sicherlich so anzunehmen. Beim Bau einer Rahmenantenne ist dieses Verhältnis aber genau anders herum. Der Durchmesser der Spule ist deutlich größer als deren Länge. Wendet man die obige Formel dennoch bei einer solchen Spulenanordnung (Rahmenantenne) an, so erhält man Induktionswerte, die schnell um den Faktor 10 zu groß sein können. In der Literatur findet man daher eine Formel zur Berechnung einer solchen kurzen Luftspule, die einen Korrekturfaktor einhält.
Wobei k der Korrekturfaktor ist, der nicht näher angegeben wird und experimentell ermittelt werden muss. OM Schau, DL3LH, gibt in einer Abhandlung über „Induktivitäten in der täglichen Amateurfunkpraxis“ Korrekturwerte für kurze Luftspulen mit einem Verhältnis von d/l bis 10 an. Bei einer Rahmenantenne für VLF kann dieses Verhältnis aber auch eventuell bei 40 liegen. Ich habe daher die Werte von DL3LH in eine Exceltabelle eingetragen und versucht grafisch weiterzuentwickeln. Das nachfolgende Diagramm zeigt das Ergebnis:
Eine so berechnete Induktivität einer Rahmenantenne entsprach zwar immer noch nicht dem gemessenen Wert, war aber immerhin schon in der gleichen Größenordnung.
Eigenkapazität
Beim Einsatz von Spulen werden gerne schon mal die Verluste einer Induktivität, allen voran die Eigenkapazität vergessen. So erging es mir bei der Konstruktion einer Rahmenantenne für VLF. Die Größe der Eigenkapazität hatte ich deutlich unterschätzt. Gerade beim Einsatz der Induktivität in einem Schwingkreis spielt die Eigenkapazität eine große Rolle. Beeinflusst sie doch die Resonanzfrequenz des Kreises. Die Eigenkapazität kann man sich als eine zur Induktivität parallel geschalteten Kondensator vorstellen. So stellt eine Rahmenantenne für sich allein schon einen Schwingkreis mit einer Eigenresonanzfrequenz dar. Diese Frequenz ist zugleich die höchste Frequenz auf die in einem Schwingkreis abgestimmt werden kann. Die Resonanzfrequenz kann messtechnisch ermittelt werden. Aber dazu in einem eigenen Beitrag mehr.
Rechnerisch lässt sich die Eigenkapazität kaum bestimmen. Als Faustformal kann angenommen werden, dass die Eigenkapazität in pF etwa dem Spulendurchmesser in cm entspricht. Aber auch dies gilt nur für Spulen bei denen ihre Länge größer als ihr Durchmesser ist. Bei anderen Anordnungen bleibt nur die messtechnische Bestimmung. Eins ist allerdings zu beobachten. Die Eigenkapazität ist proportional zum Spulendurchmesser. Beispiel: 5-facher Durchmesser bewirkt auch 5-fache Eigenkapazität.
Fazit
Eine Berechnung einer kurzen Zylinderspule ist mit dem beschriebenen Ansatz nur näherungsweise möglich. Der berechnete Wert ist aber für die weiteren Betrachtungen brauchbar und sowieso besser, als wenn man komplett im Dunkeln tappen würde.



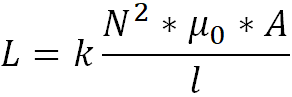








Du muss angemeldet sein, um einen Kommentar zu veröffentlichen.